Space Debris Impact on LEO Spacecraft
Introduction
Space debris, or orbital debris, is a serious threat to spacecraft in Earth orbit. These fragments, which may vary from almost invisible paint chips to defunct satellites, exist in orbits where they travel at exceptionally high speeds—fast enough to cause damage upon impact or severely compromise the performance of the affected spacecraft. It is essential to understand the probability and the nature of such impacts so that resilient spacecraft can be designed, leading to successful missions.
We shall employ a stochastic simulation approach to model and predict the probability of space debris impacting a 1U CubeSat in Low-Earth Orbit (LEO) in this study. The ESA’s MASTER (Meteoroid and Space Debris Terrestrial Environment Reference) tool allows the generation of realistic flux data for human-made debris and meteoroids. The satellite has been subjected to these threats for a period of time, and the analysis will include such key metrics as impact frequency, energy, and penetration risk.
This blog post will outline the methodology, results, and implications of the study to prepare engineering and scientific knowledge to address the challenges posed by operation in an increasingly congested orbital environment.
Methodology
Step 1: Generating Space Debris Flux Data
Satellite cross-section drag area
The cross-section of the spacecraft, computed with the ISO Standard Area (Flat Plate Model) for 1U spacecraft
\[A_{\text{ISO}} = \frac{1}{2}(xy + yz + xz)\]
The dimensions of a 1U cubesat are \[x = y = z = 0.1\text{ m}\]
Therefore
\[A_{\text{ISO}} = \frac{1}{2} (0.1 \times 0.1 + 0.1 \times 0.1 + 0.1 \times 0.1) = \frac{3 \times 0.01}{2} = 0.015 \text{ m}^2\]
Applying the correction factor1 for Cubesats to get an accurate projected area
\[A_{\text{Projected}} = 0.7295 \times A^{0.9624}_{\text{ISO}}\]
Substituting the earlier \(A_{\text{ISO}}\) value of \(0.015\text{ m}^2\) gives
\[A_{\text{Projected}} = 0.7295 \times 0.015^{0.9624}_{\text{ISO}} = 0.01281431879\]
Which gives us approximately \(0.01281 \text{ m}^2\) to 4 s.f.
Orbital Parameters
The satellite’s orbital parameters were defined as follows:
- Altitude: \(500 \text{ km}\)
- Inclination: \(97.4^{\circ}\)
- Eccentricity: \(0.01\)
- Cross-sectional area (drag): \(0.01281 \text{ m}^2\)
Flux data provides the estimates of impacts per square meter per year, the categorization done according to the particle’s diameter and source type (human-made debris or meteoroids). This information serves as the basis of our stochastic simulation.
Generate data with ESA’s MASTER
With the orbital parameters, the following distribution (flux) data was generated with the tool, with the date starting at 2025-01-01 for the duration of 5 years. 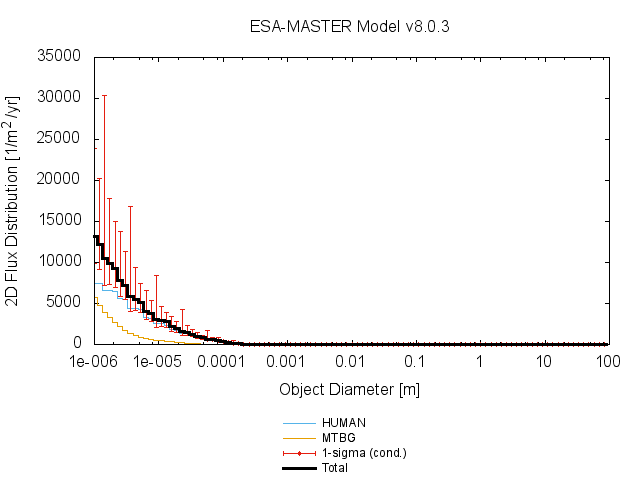
Step 2: Visualising Debris Flux Distribution
Using Python libraries like pandas, matplotlib, and seaborn, plot the flux distribution against particle diameters. The resulting graph highlights two critical trends:
- Smaller particles dominate the overall flux but carry less kinetic energy.
- Larger particles, though rarer, pose a greater threat due to their higher impact energies.
For example, our dataset revealed that: - Particle diameters ranged from \(1.1 × 10^{-6}\) meters to 91.2 meters. - Human-made debris accounted for up to 1,030 impacts/m²/year, while meteoroids contributed up to 1,010 impacts/m²/year.
These findings underscore the dual nature of the threat posed by space debris and meteoroids.
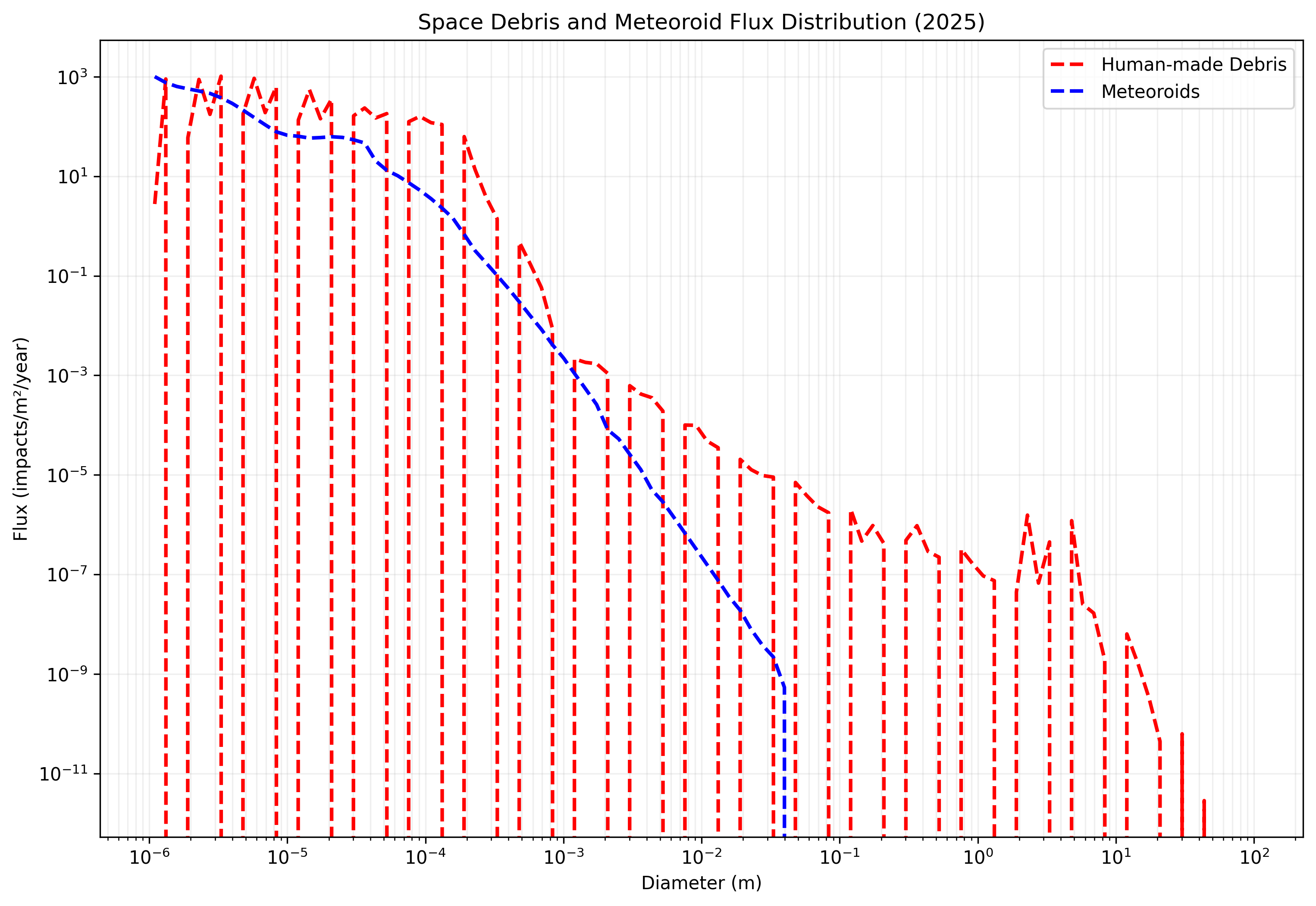
Note: Each step along the axis represents an order of magnitude change of the logarithmic scale of man-made debris.
Step 3: Running the Stochastic Simulation
Then, build a discrete-event simulation with the help of Python’s simpy library. It models some of the critical elements such as:
- Orbital Parameters: Satellite altitude, its inclination, eccentricity and the like.
- Satellite Design Parameters: Cross-section, mass, material density, wall thickness and attitude (e.g. nadir-pointing).
- Impact Dynamics: Impact velocity and penetration risk are calculated with the modified Cour-Palais ballistic limit equation for kinetic energy and impact velocity calculations.
import simpy
import numpy as np
import pandas as pd
@dataclass
class OrbitalParameters:
"""
Orbital parameters for the satellite
"""
altitude: float
inclination: float
eccentricity: float = 0.0
raan: float = 0.0
argument_of_perigee: float = 0.0
@dataclass
class SatelliteParameters:
"""
Physical parameters of the satellite
"""
cross_section: float
mass: float
material_density: float
wall_thickness: float
attitude: str
@dataclass
class ImpactEvent:
time: float
diameter: float
source: str
velocity: float
energy: float
penetration_risk: bool
class Satellite:
def __init__(self, env, flux_data, orbital_params, satellite_params):
self.env = env
self.flux_data = flux_data
self.orbit = orbital_params
self.params = satellite_params
self.impacts = []
self.orbital_period = 2 * np.pi * np.sqrt((self.orbit.altitude + 6371)**3 / 398600.4418) / 60
self.orbital_velocity = np.sqrt(398600.4418 / (self.orbit.altitude + 6371))
self.meteoroid_velocity = 20.0
self.debris_velocity = 10.0
self.action = env.process(self.run())
def calculate_impact_velocity(self, source):
"""
Calculate impact velocity based on source and orbital parameters.
"""
base_velocity = self.meteoroid_velocity if source == 'Meteoroid' else self.debris_velocity
velocity_std = 2.0 if self.params.attitude == 'tumbling' else 1.0 if self.params.attitude == 'nadir-pointing' else 1.5
return np.random.normal(base_velocity, velocity_std)
def calculate_impact_energy(self, diameter, velocity, source):
"""
Calculate impact kinetic energy in Joules.
"""
density = 2500 if source == 'Meteoroid' else 2000
mass = (4/3) * np.pi * (diameter/2)**3 * density
return 0.5 * mass * (velocity * 1000)**2
def check_penetration_risk(self, diameter, velocity):
"""
Check if impact might penetrate satellite wall using simple ballistic limit equation.
"""
critical_diameter = (0.6 * (self.params.wall_thickness**0.5) * (self.params.material_density / velocity)**(1/3))
return diameter > critical_diameter
def generate_impact_time(self, flux):
"""
Generate time until next impact using exponential distribution.
"""
hourly_flux = flux / (365.25 * 24)
rate = hourly_flux * self.params.cross_section
return np.random.exponential(1/rate) if rate > 0 else float('inf')
def run(self):
"""
Main simulation process.
"""
while True:
human_made_time = self.generate_impact_time(self.flux_data['Human_made'].sum())
meteoroid_time = self.generate_impact_time(self.flux_data['Meteoroids'].sum())
if human_made_time < meteoroid_time:
time_to_impact = human_made_time
source = 'Human-made'
diameter = np.random.choice(self.flux_data['Diameter'], p=self.flux_data['Human_made']/self.flux_data['Human_made'].sum())
else:
time_to_impact = meteoroid_time
source = 'Meteoroid'
diameter = np.random.choice(self.flux_data['Diameter'], p=self.flux_data['Meteoroids']/self.flux_data['Meteoroids'].sum())
yield self.env.timeout(time_to_impact)
velocity = self.calculate_impact_velocity(source)
energy = self.calculate_impact_energy(diameter, velocity, source)
penetration_risk = self.check_penetration_risk(diameter, velocity)
impact = ImpactEvent(
time=self.env.now,
diameter=diameter,
source=source,
velocity=velocity,
energy=energy,
penetration_risk=penetration_risk
)
self.impacts.append(impact)
def run_simulation(flux_data, duration_years=1.0):
"""
Run the satellite debris impact simulation.
"""
orbit = OrbitalParameters(altitude=500, inclination=97.4, eccentricity=0.01, raan=0.90, argument_of_perigee=0)
satellite = SatelliteParameters(cross_section=0.01281, mass=3.0, material_density=2700.0, wall_thickness=0.002, attitude='tumbling')
duration_hours = duration_years * 365.25 * 24
env = simpy.Environment()
sat = Satellite(env, flux_data, orbit, satellite)
env.run(until=duration_hours)
return sat.impactsThe simulation works like this:
- At each time step, whether the next impact results from human-made debris or meteoroids is determined.
- Select a random particle size according to the flux distribution.
- Calculate the impact velocity, energy, and the potential for wall penetration.
- It goes on until the given simulation time has been fulfilled.
The simulation simulates impacts of debris for one year.
Results
After simulating one year of operation, the following key results emerged:
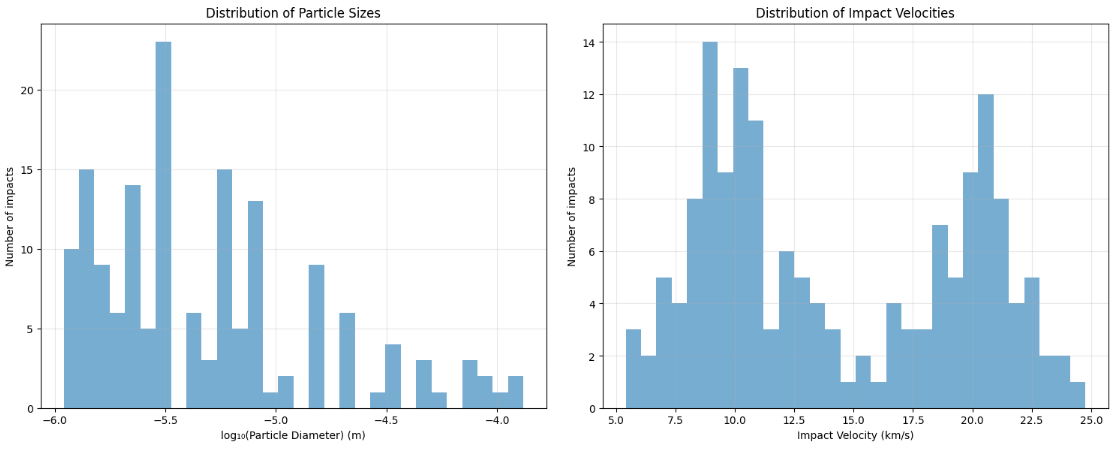
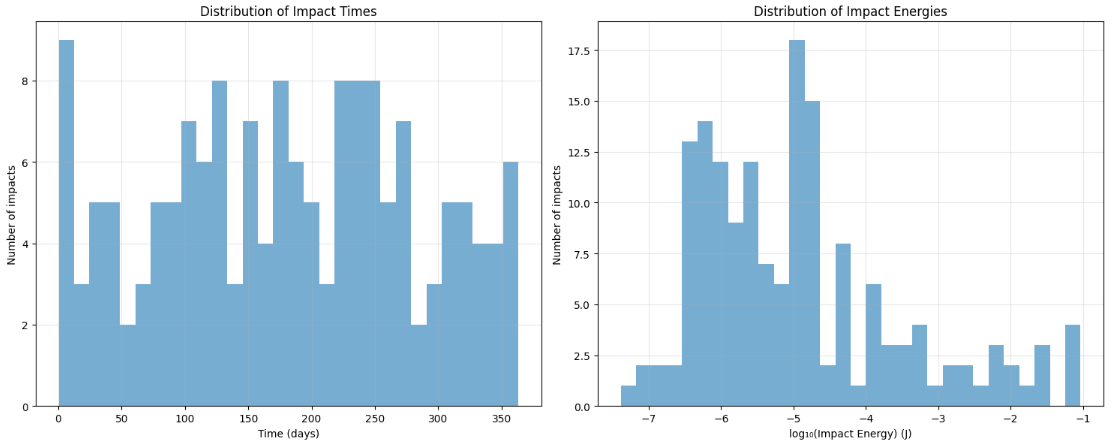
Total Impacts: The satellite experienced 120 impacts, with nearly equal contributions from human-made debris (62 impacts) and meteoroids (58 impacts).
Particle Size Distribution:
- Average particle diameter: 0.000012 meters (12 micrometers).
- Largest particle: 0.000132 meters (132 micrometers).
Impact Velocities:
- Mean velocity: 14.28 km/s.
- Maximum velocity: 24.76 km/s.
Kinetic Energy:
- Most impacts involved very low energies (< 1 Joule), consistent with the prevalence of small particles.
- One notable exception was a maximum recorded energy of 0.36 Joules, which could potentially damage sensitive equipment.
Penetration Risk: None of the simulated impacts exceeded the critical threshold required to penetrate the satellite’s walls, thanks to its robust design featuring a 2 mm thick aluminum shell.
Mean Time Between Impacts: On average, the satellite faced an impact every 2.30 days.
Discussion
The simulation investigated varying interactions among particle size, particle speed, and impact energy. Most impacts involve benign microsized particles, and when larger objects are involved, even rare impacts can wreak havoc. Thus, the designer of any LEO-leading mission will have to concentrate on shielding measures and redundancy.
Furthermore, the near-equal ranking of discarded satellites and meteoroids impels one to look at both natural and anthropogenic threats. Important efforts for diminishing space debris, including active removal campaigns and stringent disposal satellite regulations, are vital to defend future missions.
Conclusions
This project shows the importance of stochastic simulations of debris risk assessment. Real flux data in combination with advanced modeling give an insight into the very real hurdles being faced by spacecraft in LEO. As humanity starts to navigate and utilize outer space, tools like this will play an important role in safe and sustainable operation.
Footnotes
Kerr, E., & Macdonald, M., 2015. IAC-15-A6.4.6 Page 1 of 6 IAC-15-A6.4.6 IMPROVING THE ACCURACY OF GENERAL PERTURBATIONS METHODS FOR SPACECRAFT LIFETIME ANALYSIS.↩︎