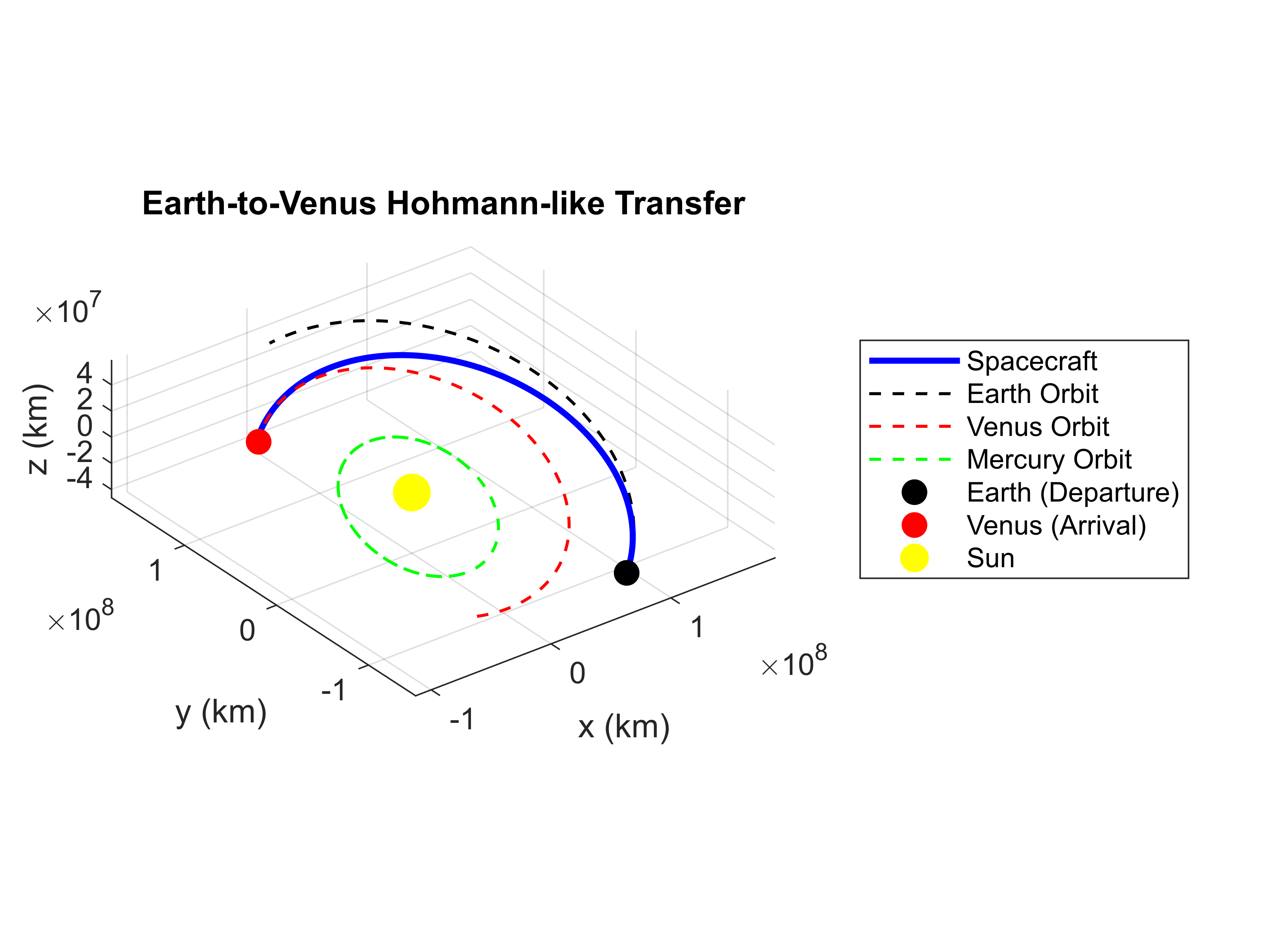
Hohmann transfer from Earth to Venus.

Launch window and Hohmann Transfer to Venus with Matlab.

Hohmann Transfer to Venus

Orbital Elements for Objects in the Solar System

Celestial Body	Semi-major axis (km)	Perihelion (km)	Aphelion (km)	Period (days)	Velocity (km \({\textrm{s}}^{-1}\) )	Eccentricity	Inclination (degrees)
Venus	\(\displaystyle 1.08209\times 10^8\)	\(\displaystyle 1.07477\times 10^8\)	\(\displaystyle 1.08940\times 10^8\)	224.7	35.02	0.00676	3.39
Earth	\(\displaystyle 1.49598\times 10^8\)	\(\displaystyle 1.47100\times 10^8\)	\(\displaystyle 1.52096\times 10^8\)	365.26	29.78	0.01670	0.00

initialTime = datetime(2026,7,31,0,0,0);
initialTimeJD = juliandate(initialTime);

mu_sun = 1.32712440018e11;

rEarth_approx = 1.49598e8;
rVenus_approx = 1.08209e8;

Orbital periods

T_Earth = 2*pi*sqrt(rEarth_approx^3 / mu_sun);
T_Venus = 2*pi*sqrt(rVenus_approx^3 / mu_sun);

T_Earth_days = T_Earth / 86400;
T_Venus_days = T_Venus / 86400;

Semi-major axis and transfer time

Semi-major axis

\[ a_t =\frac{r_E +r_V }{2} \]

Transfer time

\[ T_t =\pi \sqrt{\frac{a_t^3 }{\mu }} \]

aTransfer = (rEarth_approx + rVenus_approx) / 2;

tTransfer_approx = pi * sqrt(aTransfer^3 / mu_sun);
tTransfer_days_approx = tTransfer_approx / 86400;

fprintf('Approx. Hohmann transfer time: ~%.1f days\n', tTransfer_days_approx);

Approx. Hohmann transfer time: ~146.1 days

Angular speeds

omega_earth = 360 / T_Earth_days;
omega_venus = 360 / T_Venus_days;

theta_venus_during_transfer = omega_venus * tTransfer_days_approx;
theta_required = 180 - theta_venus_during_transfer;

Iteration parameters

currentTimeJD = initialTimeJD;
tolerance = 0.1;
maxIter = 50;

Solve for departure date (maximize phase angle)

for iter = 1:maxIter
    [earthPos3D, ~] = planetEphemeris(currentTimeJD, 'Sun', 'Earth');
    [venusPos3D, ~] = planetEphemeris(currentTimeJD, 'Sun', 'Venus');

    % ecliptic longitudes from 3D positions
    earthLon = atan2d(earthPos3D(2), earthPos3D(1));
    venusLon = atan2d(venusPos3D(2), venusPos3D(1));

    % phase angle in [-180,180)
    phaseAngle = mod(venusLon - earthLon, 360);
    if phaseAngle > 180
        phaseAngle = phaseAngle - 360;
    end

    fprintf('Iter %d:  PhaseAngle = %.2f°,  Target = %.2f°\n', ...
             iter, phaseAngle, theta_required);

    if abs(phaseAngle - theta_required) < tolerance
        fprintf('Converged at %.2f° (Error < %.1f°)\n', phaseAngle, tolerance);
        break;
    end

    % amend new departure date
    delta_theta  = theta_required - phaseAngle;
    delta_t_days = delta_theta / (omega_venus - omega_earth);
    currentTimeJD = currentTimeJD + delta_t_days;
end

Iter 1:  PhaseAngle = -55.80°,  Target = -54.03°
Iter 2:  PhaseAngle = -53.69°,  Target = -54.03°
Iter 3:  PhaseAngle = -54.10°,  Target = -54.03°
Converged at -54.10° (Error < 0.1°)

departureJD = currentTimeJD;
departureTime = datetime(departureJD, 'ConvertFrom', 'juliandate');
fprintf('Departure time: %s\n', departureTime);

Departure time: 02-Aug-2026 07:46:02

Function for propagating transfer

function dYdt = twoBody(~, Y, mu)
    % Y = [x, y, z, vx, vy, vz]
    rx = Y(1); ry = Y(2); rz = Y(3);
    vx = Y(4); vy = Y(5); vz = Y(6);

    r = sqrt(rx^2 + ry^2 + rz^2);
    accel = -mu / r^3 .* [rx; ry; rz];

    dYdt = [vx; vy; vz; accel(1); accel(2); accel(3)];
end

Propagate and plot transfer

Transfer velocity with vis-viva

\[ v=\sqrt{\mu \left(\frac{2}{r}-\frac{1}{a}\right)} \]

[earthPos3D_dep, earthVel3D_dep] = planetEphemeris(departureJD, 'Sun', 'Earth');
rEarth = norm(earthPos3D_dep);

aTransfer = (rEarth + rVenus_approx)/2;
tTransfer = pi * sqrt(aTransfer^3 / mu_sun); 
tTransfer_days = tTransfer / 86400;

vEarth = norm(earthVel3D_dep);
vTransfer = sqrt(mu_sun*(2/rEarth - 1/aTransfer));

dV = (vTransfer - vEarth);

dir3D = earthVel3D_dep / vEarth;
% update departure velocity
v0_3D = earthVel3D_dep + dV*dir3D;

fprintf('Departure speed Earth: %.3f km/s\n', vEarth);

Departure speed Earth: 29.338 km/s

fprintf('Transfer orbit speed:  %.3f km/s\n', vTransfer);

Transfer orbit speed:  26.974 km/s

fprintf('Delta-V (should be negative for Earth -> Venus): %.3f km/s\n', dV);

Delta-V (should be negative for Earth -> Venus): -2.364 km/s

Y0 = [earthPos3D_dep(1);
      earthPos3D_dep(2);
      earthPos3D_dep(3);
      v0_3D(1);
      v0_3D(2);
      v0_3D(3)];

twoBody3D = @(t, Y) twoBody(t, Y, mu_sun);
tspan = [0, tTransfer];

opts = odeset('RelTol',1e-9, 'AbsTol',1e-12);
[t_sol, Y_sol] = ode45(twoBody3D, tspan, Y0, opts);

x_spacecraft = Y_sol(:,1);
y_spacecraft = Y_sol(:,2);
z_spacecraft = Y_sol(:,3);

Npts = 200; % n = sample points
timeArray = linspace(departureJD, departureJD + tTransfer_days, Npts);
earthXYZ = zeros(Npts, 3);
venusXYZ = zeros(Npts, 3);
mercuryXYZ = zeros(Npts, 3);

for i = 1:Npts
    [posE, ~] = planetEphemeris(timeArray(i), 'Sun', 'Earth');
    [posV, ~] = planetEphemeris(timeArray(i), 'Sun', 'Venus');
    [posM, ~] = planetEphemeris(timeArray(i), 'Sun', 'Mercury');
    
    earthXYZ(i,:) = posE(:)';
    venusXYZ(i,:) = posV(:)';
    mercuryXYZ(i,:) = posM(:)';
end

figure('Name','Earth->Venus 3D Transfer'); 
hold on; grid on;

plot3(x_spacecraft, y_spacecraft, z_spacecraft, 'b', 'LineWidth', 2);

plot3(earthXYZ(:,1), earthXYZ(:,2), earthXYZ(:,3), 'k--', 'LineWidth', 1);
plot3(venusXYZ(:,1), venusXYZ(:,2), venusXYZ(:,3), 'r--', 'LineWidth', 1);
plot3(mercuryXYZ(:,1), mercuryXYZ(:,2), mercuryXYZ(:,3), 'g--', 'LineWidth', 1);

plot3(earthPos3D_dep(1), earthPos3D_dep(2), earthPos3D_dep(3), 'ko','MarkerSize',8,'MarkerFaceColor','k');

arrivalJD = departureJD + tTransfer_days;
[venusPosArr, ~] = planetEphemeris(arrivalJD, 'Sun', 'Venus');
plot3(venusPosArr(1), venusPosArr(2), venusPosArr(3), 'ro','MarkerSize',8,'MarkerFaceColor','r');

plot3(0, 0, 0, 'yo', 'MarkerSize',12, 'MarkerFaceColor','y');

% display plot
xlabel('x (km)'); ylabel('y (km)'); zlabel('z (km)');
title('Earth-to-Venus Hohmann-like Transfer');
legend('Spacecraft','Earth Orbit','Venus Orbit','Mercury Orbit', 'Earth (Departure)','Venus (Arrival)','Sun', 'Location','eastoutside');
axis equal; 
view(3);
rotate3d on;
hold off